The Value of a Hole in Coal: Assessment of Seasonal Thermal Energy Storage and Recovery in Flooded Coal Mines

Introduction

One of the major challenges for the ongoing energy transition is the decarbonisation of the space heating sector, a major CO₂ emission source (Sansom, 2015; Watson et al., 2019) which amounts for 51% of the global energy consumption (REN21, 2019). In high-latitude countries, such as the United Kingdom, this sector experiences a strong seasonal fluctuation that evidences the need for large-scale energy storage strategies (Figure 1) for a decarbonisation process with renewable sources of energy. At present, increasing the exploitation of shallow low-enthalpy geothermal resources is being considered among other alternatives, such as green hydrogen and solar heating applications (Dodds and Demoullin, 2013; Dahash et al., 2019), to reduce the carbon intensity in combination with district heating networks (Sayegh et al., 2017). However, the exploitation of geothermal resources in large-scale open-loop schemes requires a considerable groundwater flow (Bertermann et al., 2015) and the proximity of the heat resource to the potential users (Menéndez et al., 2020).

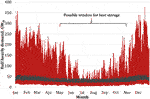
FIGURE 1. Half-hourly heat demand (red) and electricity demand (grey) in the UK for the year 2010. This chart, of Sansom (2014), illustrates with the large seasonal fluctuation in energy demand related to space heating. A potential window for thermal energy storage is delineated around summer months.

Over the past 200 years, coal mining has left exceptional hydraulic conditions in the subsurface of thousands of sites often situated under urban areas, that may allow water extraction rates above 100 m³ h⁻¹ (Fernandez-Rubio and Lorca, 1993). Of the seven mine-water geothermal plants in operation globally, the two schemes with the highest installed capacity (>500 kW) are located in flooded coal mines of Asturias, Spain, and Heerlen, Netherlands (Menéndez et al., 2020). The mine-water project of the Barredo Shaft in Asturias (∼3,500 kW) was installed in 2012 for space heating and cooling of a hospital located at 2 km from the coal mine, with an average mine-water temperature of 23°C. The potential expansion of this type of systems is restricted by the natural heat resource in place, typically with associated Carboniferous formations at shallow depths and groundwater temperatures below 30°C (Peralta Ramos et al., 2015).

Aquifer thermal energy storage (ATES) techniques, that involve the use of solar thermal collectors or waste heat from industrial operations (Fleuchaus et al., 2018; Pellegrini et al., 2019), could be employed to increase the installed capacity and prevent an early depletion of the heat resource. The third phase of the Heerlen mine-water project (Minewater 3.0) incorporates a fifth-generation district heating and cooling system, in which residual heat from industrial processes and space cooling is injected into a network of interconnected legacy coal mines functioning as a heat sink (Boesten et al., 2019). This project, in operation since October 2008, has resulted in a reduction of approximately 50% of the CO₂ heat-related intensity in the heating and cooling grid (Verhoeven et al., 2014). Another important mine-water scheme is the German HEATSTORE project in the city of Bottrop, where water heated by solar thermal collectors is injected into an underground coal mine during summer months, for its extraction during winter to heat the buildings of the International Geothermal Centre (Hahn et al., 2018).

Forecasting the performance of these systems is a complex task given the typical intricacy in the layout of underground coal mines, as well as possible georeferencing imprecisions and lack of official record of some mine workings (Bell and De Bruyn, 1999). The subsurface void system typically includes shafts, roadways and coal extraction panels, whose geometry depends on the mining method applied. Traditionally, the room-and-pillar and longwall techniques have been the preferred methods for mining flat-dipping and tabular deposits such as coal seams (Okubo and Yamatomi, 2009). The longwall method is a highly mechanized technique, mostly applied post-1950s to mine relatively deep coal seams while achieving a high coal extraction ratio (>70%) associated with an instant roof collapse (Bell et al., 2000; Lehmann et al., 2017).

On the other hand, the room-and-pillar method achieves a lower coal recovery ratio (typically from 30 to 70%) due to the inclusion of pillars to prevent roof collapse (Ullah et al., 2018); although recovery ratios higher that 70% could be reached if retreat mining is employed (Scott et al., 2010). Due to the widespread application of this technique in mining the shallower coal seams (<300 m), it represents a large portion of accessible voids for potential underground thermal storage. This is particularly true for countries with an extensive record of coal mining such as the UK where, for instance, Gluyas et al. (2020) estimated a theoretical thermal energy storage potential for abandoned mines of approximately of 32 TWh with a 10°C change in mine-water temperatures.

The prospectivity of the subsurface voids depends on the hydraulic conditions in place, which could be potentially affected by anthropogenic material filling, clay-rich coal breccia sedimentation and roof collapse (Andrews et al., 2020). The latter could result in fracture networks around extraction panels, as evidenced in the exploration results of the Glasgow Geoenergy Observatory (Monaghan et al., 2021), that could increase the “effective thermal conductivity” of the host rock, i.e., rock mass surrounding the mine voids, and improve the subsurface heat transport (Chiasson et al., 2000). Additional adverse effects that could constrain the exploitation of the heat resource include: high water pumping costs and corrosion of the installations (Walls et al., 2021), iron oxyhydroxide precipitation (Banks et al., 2019), potential surface alterations due to mine-water level changes (Todd et al., 2019) and hypersaturation of calcite (Jagert et al., 2018). On a large scale, the regional groundwater flow could result in an unwanted dispersal of heat if the location of injection and extraction boreholes is not properly optimized (Raymond and Therrien, 2014); particularly, in flooded panels with a strong hydraulic connection with shallow aquifers or surrounded by thermally conductive lithologies, as is the case of the Glasgow Main Coal (Monaghan et al., 2021).

Generally, the thermal conductivity of dry sedimentary rocks ranges from 0.5 W m⁻¹ K⁻¹–4.5 W m⁻¹ K⁻¹ (Rühaak et al., 2015); coal has an exceptionally low matrix thermal conductivity (<0.6 W m⁻¹ K⁻¹) that could hamper the formation of a thermal reservoir in the subsurface. Additionally, the thermal storage capacity (ΔQ) of the host rock (Eq. 1) could be affected by the low density (ρ) of coals despite having a characteristic high specific heat capacity (c) (Waples and Waples, 2004). Insulating conditions can also occur in mine workings surrounded by thick organic shales, which would slow heat transport and reduce the thermal storage capacity of the system (Labus and Labus, 2018).

The review of Loredo et al. (2016) revealed that only a small number of published studies have investigated the particular geothermal characteristics of flooded coal mines through numerical modelling, evidencing the relatively “unexplored” character of this subject in geoscience literature. More recently, a few modelling studies have advanced in the understanding of important aspects, such as the hydraulic interaction between different void structures in flooded coal mines (e.g., Díaz-Noriega et al., 2020). Therefore, as these systems have not been thoroughly examined and limitations for their numerical simulation have also been documented (Renz et al., 2009), additional studies would be beneficial for the evaluation of the unique subsurface conditions.

In this context, this investigation aims to improve the understanding of heat transport in coal-mine environments through the simulation of a generic mine-water scheme in a 3D model of a flooded room-and-pillar panel. The conceptual model is a simplification of a possible real-world operation that would involve multiple injection/extraction boreholes or changes in the temperature of the injected water, which are not included in the models. The simulation results, which could be up-scaled for specific sites, are used to assess the following critical aspects for the performance of mine-water thermal schemes:

⁃How the thermal properties of the rock mass (e.g., thermal conductivity, specific heat capacity) influence the heat storage capacity in the system

⁃The maximum achievable energy retrieval from the subsurface with cold-water refill cycles

⁃The effect of hydraulic power consumption, related to water pumping, in the energy balance of the thermal storage system

⁃A financial comparison of the heat recovered from the subsurface with coal and other energy sources used at present for space heating, with reference to the UK energy prices.

Methods

A seasonal layout of two 6-month phases, representing a simplified heat demand in high-latitude regions (Figure 1), was designed for the simulation of the mine-water thermal storage scheme of Figure 2. The first phase—heat storage—represents the period of elevated solar intensity and low heat demand around summer months, which would make possible the subsurface injection of heated water and thermal storage in the host rock. Subsequently, water extraction and cold-water reinjection, aimed at retrieving the stored heat with ground-source heat pumps, would take place around winter months to meet the increased space heating demand. The modelled storage space corresponds to a 60 m × 60 m room-and-pillar panel with no roof collapse or material filling, which represent prospective conditions for mine-water thermal schemes. The room-and-pillar panel contains nine 12 m × 12 m pillars and has a total void volume of 2340 m³, which includes part of the extraction borehole.

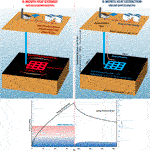
FIGURE 2. Conceptual model of the mine-water thermal storage scheme with the key boundary conditions (BC) and initial condition (IC) set in the modelling software (OpenGeoSys), as well as the energy graph of the potential evolution of rock thermal energy and mine-water temperature during the heat storage and extraction phases. The system would be associated with a potential district heating network and thermal energy harvested from industrial “waste” heat, solar thermal collectors or space cooling during periods of low heat demand.

While the model was designed with typical dimensions and geological properties found in legacy coal mines, this study does not intend to reproduce the settings of a particular site; instead, it aims to model conditions that could be considered prospective for potential mine-water schemes, e.g., a large inter-connected void space and limited interaction with surface recharge. Nonetheless, several other conservative assumptions are set in the models, such as a moderate geothermal gradient, and a scenario with pessimistic thermal properties is investigated.

For the numerical simulation of subsurface heat transport, the open-source modelling software OpenGeoSys (https://www.opengeosys.org/) was employed, which applies the finite element method for the approximation and numerical solution of the heat balance partial differential equation. This relationship (Eq. 2) describes the spatial temperature distribution (T) in a porous medium, comprising the conductive and advective components of heat transport for solid and fluid phases, with a bulk and pore-water density (ρ_b and ρ_w), bulk and pore-water specific heat capacity (c_b and c_w), Darcy velocity (v), and in the presence of a heat source or sink (q). The term D corresponds to the bulk thermal diffusivity, which is proportional to the thermal conductivity (λ_b) of the porous medium (Eq. 3).

Where in this case Δ is the Laplace operator, ∇ is the Nabla operator and I is the identity matrix.

For the simplification of the numerous time-consuming simulations required, quasi-stationary groundwater flow conditions are established in the numerical model, i.e., conductive heat transport is simulated and the effect of local advection is not modelled. This could be considered a conservative assumption with respect to the potential recovery of stored heat, since numerous numerical modelling and experimental studies have demonstrated the enhancing effect that advection has around geothermal wells in high-permeability settings (Diao et al., 2004; Zhou et al., 2013; Choi et al., 2013). On the other hand, as heat conduction in sedimentary rocks takes place both in rock-forming minerals and water in pore spaces, unlike solute transport, it has been shown to be the dominant thermal transport mechanism for typical hydraulic gradients scenarios (0.01—0.0001) in consolidated rocks (Ferguson, 2015). Thus, heat conduction would be the predominant heat transport mechanism outside the anthropogenically altered rock mass and advection would have an important role in the disturbed volume, which is further analysed in the Discussion section.

As illustrated in Figure 2, a constant surface temperature of 9°C is set as a (Dirichlet) boundary condition and a geothermal gradient of 20°C km⁻¹ is applied as initial condition, which gives the flooded room-and-pillar panel, at a depth of 150 m, an initial temperature of 12°C. This geothermal configuration could be considered a modest assumption even for high-latitude countries such as the UK, where coal fields evidence geothermal gradients in the range of 17.3–34.3°Ckm⁻¹ (Farr et al., 2020). The 6-month heat storage phase is simulated with 50°C constant-temperature boundary conditions around the extraction panel, representative of sufficient heat harvested and continuously injected to the subsurface to maintain a stable thermal state in the mine water.

The heat extraction phase, encompassing cold-water refills, is modelled with a “restart” that cyclically sets the mine-water temperature to 12°C and symbolises the extraction of the 2340 m³ of water and refill with water at the initial geothermal temperature. Seven different interval lengths for the cold-water refills are modelled in the heat extraction phase, ranging from 1 to 182 days, to measure the change in energy recovery with this parameter. Each refill cycle comprises the extraction of a total volume of water in the 6-month heat extraction period and an equivalent pumping rate, shown in Table 1. In addition to the 1-year periods modelled, a 5-year simulation of a medium efficiency cycle (14-days refill interval) is computed to evaluate the long-term evolution of the system. Since the modelled instantaneous cold-water refill, aimed at reproducing the exceptionally high transmissivity of flooded mine workings (e.g., > 2000 m²/d; Shorter et al., 2021), results in relatively high heat fluxes from the host rock towards the mine water, the modelling results are interpreted as the maximum energy that could be retrieved from the system.

TABLE 1. Cold-water refill intervals modelled in heat extraction phase with the cumulative volume of water extracted in each refill cycle for the 182-day period.

The strong interstratification normally observed in coal-bearing sections, that could contain intercalations of sandstone, shale and palaeosol layers, in addition to the distinctive thermal properties of coals, could lead to challenges for heat transport simulations in these settings (Wen et al., 2015; Andrés et al., 2016). Coals can display half the density and a sixth of the thermal conductivity of typical sedimentary rocks, whose properties normally overlap (Vasseur et al., 1995; Waples and Waples, 2004). With this in consideration, an initial sensitivity analysis was conducted – prior to the 3D numerical simulations – in a 1 m thick horizontal slice of the mine workings (Figure 3) setting two different host rocks around the flooded panel: a coal seam (real-world situation) and a “Characteristic” Sedimentary Rock (CSR).

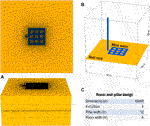
FIGURE 3. Section of the numerical mesh of prism-shaped elements used in the simulations (A); 2D slice used in the host-rock sensitivity analysis (B), and geometrical configuration of the 1 m thick generic room-and-pillar panel (C).

The thermal properties assigned to these two host rock materials were gathered from existing literature for conditions potentially found in legacy coal mines. For the specific heat capacity, a value of 800 J kg⁻¹ K⁻¹ was set for the CSR material according to the 700–900 J kg⁻¹ K⁻¹ range considered as typical for the majority of rock-forming minerals (Waples and Waples, 2004). These authors also report a higher average specific heat capacity for coals, ranging approximately from 1000 to 1400 J kg⁻¹ K⁻¹, thus, an individual value of 1200 J kg⁻¹ K⁻¹ was chosen for this material. Regarding the thermal conductivity of dry sedimentary rocks, according to Alishaev et al. (2012), sandstones generally show values well above 3 W m⁻¹ K⁻¹ due to the high thermal conductivity of quartz. The study of Tang et al. (2019) reports mean thermal conductivities for sandstones and shales of 3.06 and 2.57 W m⁻¹ K⁻¹, respectively, limestones and dolomites of 2.53 and 3.55 W m⁻¹ K⁻¹, respectively; and a mean value for all studied rocks of 2.85 W m⁻¹ K⁻¹. Busby (2019) estimated thermal parameters of the formations underlying the Glasgow Geoenergy Observatory and reported representative values for Carboniferous sequences such as the Scottish Coal Measures (2.02 W m⁻¹ K⁻¹) and the Passage Formation (2.9 W m⁻¹ K⁻¹); specifically, for the middle section of the Scottish Coal Measures they report an average thermal conductivity of 3.58 W m⁻¹ K⁻¹ for sandstones and 2.23 W m⁻¹ K⁻¹ for siltstones, which are the lithologies with the highest number of measurements (boreholes located in Northern England). As these values are commonly reported in the literature, a representative value of 3 W m⁻¹ K⁻¹ was chosen for the “Characteristic” Sedimentary Rock material.

For the coal material, a value of 0.35 W m⁻¹ K⁻¹ was considered as representative, given the range of thermal conductivities normally reported in the literature (e.g., 0.22–0.55 W m⁻¹ K⁻¹; Herrin and Demirig, 1996). The “fully-saturated” thermal properties of the two host-rock materials (density—ρ, thermal conductivity—λ, specific heat capacity—c) were calculated with Eqs 4–6 for three different porosity (Φ) values: 0.05, 0.15 and 0.25 (Table 2). This porosity variation aims at quantifying the sensitivity of the model to different pore-water content in the host rock, given the extremely high specific heat capacity of water (≈4200 J kg⁻¹ K⁻¹) and the typical presence of fractures around coal extraction panels. In this regard, the extent of these networks (rarely affecting near-surface levels) is related to aspects such as the thickness of the worked seam to pillar width, the depth below surface and type of roof strata (Bell et al., 2000). In the case of roof collapse, the rock volume experiencing substantial sagging and extensional fracturing, thus, large increase in void space, would extend over a vertical distance of one-third of the horizontal extent of the collapse zone, which could correspond to the extent of a localized pillar collapse or to a whole longwall extraction panel (Younger and Adams, 1999).

TABLE 2. Material properties assigned to the host rock in the numerical simulations. The “saturated” values for the three porosities modelled (0.05, 0.15, and 0.25) were used in the 2D sensitivity analysis and the values corresponding to the porosity of 15% (bold) were set for the geologic materials in the 3D model of the mine-water system.

The geological configuration of Figure 4, used for the simulation of the 3D mine-water scheme, consists of a single coal layer vertically aligned with the room-and-pillar panel and embedded in a volume of the CSR of ø = 0.15. The single porosity value of 15%, used for the calculation of the set of “saturated” thermal properties in the 3D model (Table 2), was chosen as a simplified representation of the potentially increased void space around worked coal seams by fracture and cleat networks.

FIGURE 4. Geological configuration of the 3D models used to investigate the effect that minor lithological changes (e.g., coal thickness) have in the performance of the geothermal scheme.

Two models of different coal thickness were used to evaluate how this minor stratigraphic change in the host rock would affect the subsurface heat storage. As the thickness of mined coals typically ranges from 0.5 to 2 m (Bell et al., 2000), a 1 m coal layer – of same thickness as the extraction panel—was defined for the favourable scenario (Model A) in which the mine voids are in direct contact with the coal-free rock volume. In Model B—adverse scenario—the panel is fully embedded by an (exceptionally thick) 3 m coal layer, which would represent an atypical situation in coal mines, as the height of the extraction panel normally equals the coal bed thickness. The inclusion of this pessimistic scenario aims to account for non-prospective conditions in worked panels, such as the presence of thick shale layers adjacent coal seams or partial sedimentation of clay-rich material in the mine voids, which would decrease the thermal transport to the host rock. Since the two modelled scenarios could be considered opposite, the modelling results are used to establish a range of feasible heat recovery outcomes for the generic scheme analysed. However, it should be noted that, since prospective thermal and hydraulic conditions are desirable for the establishment of a subsurface heat reservoir, the results of Model A should be considered more representative of efficient mine-water thermal schemes.

The thermal energy in the rock volume and groundwater is computed with daily time-steps for each scenario modelled and the start-end energy difference in the rock volume, denoted as Energy Retrieved in Figure 2, is measured to obtain the total heat retrieval percentage using Eq. 7. For this calculation, a recovery of 100% would correspond to scenarios where all the energy transferred to the subsurface was recovered with cold-water refills.

The hydraulic power required for the operation, i.e., energy potentially consumed in water pumping, was calculated with Eq. 8 using the water extraction rates of Table 2, a standard value of 0.7 for Pump Efficiency (Kaya et al., 2008) and three Δh values (25, 75, and 125 m) to investigate the effect of this critical parameter for sites with a rebounding water table. The resulting Hydraulic Energy is then subtracted from the Energy Retrieved (from the subsurface) to obtain the seasonal Net-Energy gain, applying Eq. 9, which constitutes the energy balance in the scheme. It should be noted that other factors beyond the scope of this investigation, such as ground-source heat pump thermal boost or energy losses in pipeline circulation, should be included in future studies for a more precise estimation of the energy balance in the heat storage system.

Finally, the Net-Energy values of each operational year, are used in Eq. 11 to estimate the time it would take for the cumulative heat recovered from the subsurface to reach the theoretical energy value of the coal ‘mined’ from the 2340 m³ of subsurface voids. The density (ρ) assigned to the coal layer in the 3D numerical model (ø = 15%, Table 2) is used for the Coal Energy calculation (Eq. 10) with a theoretical value of 2.65 MJ kg⁻¹ for the Gross Calorific Value, which corresponds to the average of all coal consumed in UK’s power stations in 2019 (Department for Business, Energy and Industrial Strategy, 2020a). The Number of Years estimation could be considered conservative, given that a constant first-year performance is assumed in the calculation and the 5-year simulation shows that the scheme performance improves annually (Figure 10).

Results

2D Sensitivity Analysis

The results of the initial sensitivity analysis, applying a single cold-water refill at the end of the heat storage cycle, show the expected contrasting thermal response of coals with that of other typical sedimentary lithologies. As shown in the temperature distribution maps of Figure 5, at the end of the 6-month heat storage phase, the CSR host rock stores twice the energy of the coal case, which has a significantly smaller temperature anomaly inside the pillars and around the panel. On the other hand, the modelled 5-fold increase in porosity in the host rock (0.05–0.25) only increases by 16% and 5% the heat stored in the coal and CSR scenarios, respectively.

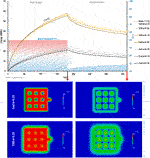
FIGURE 5. Energy evolution of the six planar models simulated in the 2D sensitivity analysis of host-rock type and increase in pore-water content (5, 15, and 25 %). The temperature maps, which correspond to the ø = 0.15 scenario (slice depth = 150 m), illustrate the difference in heat transfer produced by the contrasting thermal properties between the coal and CSR planar models.

These results highlight the primary role of rock-forming minerals and the smaller impact of pore-water content for the magnitude of the conductive heat transport and thermal storage in the host rock. Should fracture networks around extraction panels be modelled as high-permeability zones in coupled hydraulic-thermal simulations, the results could show higher rates of heat storage and extraction, as the effective thermal conductivity of the host rock is increased (Chiasson et al., 2000). It is in this anthropogenically altered rock volume where advection would have the largest impact on the performance of the mine-water system; outside this area, heat conduction would be the main mechanism for thermal transfer (for typical scenarios of hydraulic gradients <0.01) and advection would have a much smaller role proportional to the regional groundwater flow (Ferguson, 2015).

3D Mine-Water Scheme Simulation

Small lithological variations could have a large effect in the thermal recovery from the subsurface, as evidenced in the results of the 3D simulation of the mine-water scheme of Figure 6. In the favourable scenario (Model A–green), 163% more energy is stored in the subsurface during the heat storage phase due to the direct contact of the mine voids with the dense and more thermally conductive CSR rock volume. This supports the identification of surrounding strata rich in thermally conductive minerals, e.g., quartz or dolomite, as positive indicators for thermal storage in scenarios of considerable surplus heat available for subsurface injection.

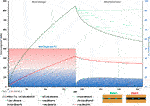
FIGURE 6. Host-rock energy evolution of four of the seven refill frequencies modelled in the two scenarios of the mine-water thermal storage scheme. The mine-water temperature of the single-refill cycle (182 days) in Model B is included for reference.

During the heat extraction phase, the energy recovery increases significantly with shorter cold-water refill intervals and the peak temperature reached in each successive cycle progressively declines. An inflection in the average mine-water temperature occurs during the longest refill intervals related to the transient spread of heat outside the mine voids and loss of energy in the mine water at late times. As evidenced in Figure 6, it occurs in day 248 in Model B, later than in Model A (day 208), due to the thick embedding coal layer slowing heat transport in the system. This insulating effect of coals, albeit unfavourable for the subsurface thermal storage capacity, would be beneficial for scenarios of low availability of harvested heat for subsurface injection.

At the end of the 1-year period, a considerable amount of energy is still left unrecovered in the subsurface even with the most intensive cold-water refill cycles modelled, as evidenced in Figure 7 (Heat Extraction – End). This constitutes the principal energy loss in the system, which could be in minimized in a real-world operation, including multiple heat extraction/injection locations, through a layout of boreholes according to the regional groundwater flow (Raymond and Therrien, 2014).

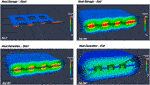
FIGURE 7. Clipped volumetric contours of the 7-day refill cycle in Model A; showing the thermal state around the mined panel at the beginning and end of the first-year of heat storage and extraction phases.

Energy Efficiency Assessment

A maximum of 25%–45% of the energy transferred to the subsurface was recovered with cold-water refills in the modelled 1-year operation of the different scenarios analysed. While the heat extraction percentage improves with cycles of higher frequency, which counter the heat dispersal outside the room-and-pillar panel area, the deceleration observed at the highest frequencies points to a practical limit in the energy potentially recovered from the subsurface (Figure 8). This plateau, related to progressively smaller gains in the heat recovery with increasingly shorter refill intervals, is reached earlier in Model B due to the insulating properties of the thick coal bed.

FIGURE 8. Percentage of total heat recovery (from the host rock) achieved in the extraction phase for the different refill intervals modelled (Δh = 25). The bubble area represents the amount of energy extracted in each scenario.

Since intensive water extraction and injection operations—modelled as shorter refill intervals—involve a greater hydraulic energy consumption (Table 3), the efficiency of the thermal scheme could be substantially reduced in cases of low energy stored in the subsurface. Elevated hydraulic power requirements could result in negative energy balances in the system, where less energy is recovered from the subsurface than is consumed in water pumping from deep water tables. However, should the thermal boost of ground-source heat pumps be applied to the final mine-water temperatures, none of the modelled scenarios would produce negative energy yields in the annual operation, as was the case of the deep water tables in Model B (Figure 9).

TABLE 3. Energy results of the 3D scheme simulation for the two geological scenarios modelled (Δh = 25 m).

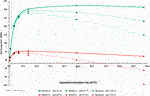
FIGURE 9. Net-Energy recovered for each refill interval modelled (graphed by its equivalent water extraction rate). This Net-Energy estimation (Eq. 9) includes the hypothetical energy consumption in water pumping (hydraulic power) for the three Δh evaluated.

Long-Term Scheme Operation

The five-year simulation of a medium-efficiency cycle shows that the progressive temperature increase in the subsurface results in a higher thermal contrast between the host-rock and water refills that improve the scheme performance every year (Figure 10). This annual increase in the energy retrieval diminishes as the thermal conditions in the subsurface approach a quasi-steady state and the system evolves into a thermal equilibrium. In the modelled scenario (14-day refill cycle), the heat retrieval percentage surpasses 50% after 3 years of operation, as the thermal reservoir is gradually established in the surroundings of the flooded mine.

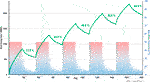
FIGURE 10. Thermal energy evolution of the rock volume (green) with the percentage of energy recovery reached in each heat extraction phase and mine-water temperature (colour shaded) for the five-year simulation of the 14-day refill cycle in Model A.

Coal Energy Analysis

The first-year Net-Energy recovery results of Table 3 are used as fixed values in Eq. 11 to compare the low-enthalpy heat provided by the mine-water thermal scheme with a high-density energy source, such as coal. The results of Figure 11 show that it could be possible to retrieve from the subsurface the (theoretical) 22550 MWh in the 2983.5 t of ‘mined’ coal in less than 70 years, for the scenarios of Model A. A broader and more conservative interpretation of the results points to the 100–300 years range as a feasible timespan for the cumulative heat recovered from the subsurface to reach the total gross calorific value of the ‘mined’ coal. Although this estimation is related to the conceptualization of the system, as well as assumptions in the numerical model, it is useful to illustrate how the seasonal heat storage technology compares to coal, a historically used energy source which would be physically linked to the mine-water scheme.

FIGURE 11. Number of years for the cumulative Net-Energy recovered in each scheme modelled, to reach the theoretical energy of the 2983.5 t coal “mined” from the room-and-pillar panel, assuming a constant first-year performance.

Finally, the financial analysis of Figure 12 aims to compare the heat retrieved from the scheme with natural gas and electricity, the sources of energy most frequently used for heating at present. With data from the (Department for Business, Energy and Industrial Strategy, 2020) of UK Energy Statistics, a hypothetical market price of the 2983.5 t of the ‘mined’ coal was estimated using the five-year average (2015–2019) of all coal purchased by power producers in the United Kingdom. Similarly, the unit value of energy (£·kWh⁻¹) of electricity and natural gas was estimated with the 5-year average (2015–2019) of the price paid by non-domestic (industrial) consumers in the country. Then, the monetary value of the Net-Energy recovered seasonally in a medium efficiency scenario (i.e., 14-days refill cycle), could equal the financial worth of the “mined” coal in 25 years using gas prices and in 5 years with electricity prices, i.e., assigning a low and high energy price for the recovered heat, respectively. Should the thermal evolution of the 5-year simulation be considered, this illustrative financial association could result in a more favourable outlook for the modelled scheme.

FIGURE 12. Illustrative financial analysis of the heat recovered in the 14-day refill cycle of Model A with a hypothetical monetary value of the “mined” coal, assuming a constant first-year energy recovery. Energy price source: Department for Business, Energy and Industrial Strategy (2020b).

Discussion

Modelling thermal processes in flooded underground coal mines is a non-trivial challenge due to the heterogeneous conditions of the subsurface voids, the uncertain extent of mining-induced fracture networks and current lack of available data for model calibration. Representing the contrasting scale of flow regimes with a continuum approach is particularly challenging, given the refinement level necessary for the numerical models. Therefore, the conceptualization of the system involves a simplification of its intricate and heterogeneous nature (e.g., local geology and void geometry), as was the case of this study, in order to reduce the computational efforts required to obtain accurate forecasts of long-term operations. Since this study aims at quantifying the subsurface heat recovery in generic scenarios, i.e., the conditions of a real-world site are not simulated, the size of the 3D numerical mesh is orders of magnitude smaller that the potentially used to characterize large-scale mine-water thermal schemes. Therefore, open-loop schemes placed in areas with large interconnected subsurface voids, compared to the distribution of heat injection/extraction locations, would take longer to evolve to a quasi-steady thermal state compared to the modelling results of this investigation.

By way of illustration, we examine the potential characteristics of modelling of a mine-water thermal scheme in the documented mine workings of the Glasgow Main Coal at the UK Geoenergy Observatory. The corresponding 3D model would likely require a surface extension much larger than 1 km² to be representative of the worked area, which would include dozens of pillars (see mine plan images in Monaghan et al., 2021). For this particular coal seam, the hydraulic connection with other levels could be assumed as minor, as shown by the results of initial pumping tests (Shorter et al., 2021). High coal extraction ratios, as the value modelled in this study (64 %), could be applicable to many zones of the Glasgow Main Coal given the large “total extraction areas” described in the mine abandonment plans, the competent sandstone roof overlying the coal seam and the open working character evidenced in the caliper logs and optical images of the site investigations. However, a considerably lower void volume should be modelled in areas with an expected collapse of the sandstone roof or with presence of backfilled mine waste. Still, a very high hydraulic conductivity should be set for these “low-prospectivity” areas, given the considerable groundwater flow evidenced in initial pump tests, some of which were performed on boreholes screened across fractured and partial coal pillars in the Glasgow Upper Coal (Shorter et al., 2021).

In spite of the generic nature of this study, our research highlights many essential aspects for thermal storage in legacy coal mines, such as the large impact that small lithological variations have in subsurface heat transport related to the physical properties of coals. The results indicate that the characteristics of the host rock should be represented in detail for an accurate forecast of these systems, to the detriment of the computational efforts required. The simulations also confirm the considerable amount of heat unrecovered from the subsurface in a potential real-world operation (related to the achievable thermal flux from the host rock) even in prospective subsurface conditions and intensive cold-water circulation operations. This aspect is of major importance for future modelling work and for the planning and optimization of potential mine-water thermal schemes.

Regarding the financial analysis based on the UK energy prices, as many capital expenditure costs are not considered (e.g., exploration, drilling or heat distribution costs), the results should be regarded as an illustrative and comparative appraisal of the financial value of the energy sources currently used for space heating. Logically, assigning energy prices of natural gas and electricity to the heat recovered from the subsurface is not a rigorous supposition, nor is the assumption of a constant energy price in time. In spite of this, the results could be used to gain a general perspective of the technology versus “expensive” and “cheap” energy options available for heating, and the value of legacy coal mines in the context of the current global decarbonisation push.

Given the generic character of the scenarios modelled and the numerical simplifications described in the Methods section, the following critical limitations should be considered when analysing the results of this study:

Potential Effect of Advective Heat Transport

The relative contribution of advection and diffusion in subsurface heat transport is a complex and often uncertain aspect for the appraisal of geothermal systems in heterogeneous formations. The literature is generally dominated by studies where advection (and dispersion) is assumed to have a minimal role, in order to simplify the simulation of subsurface heat transport. This approach has been shown to be convenient for estimating the performance of closed-loop systems (borehole heat exchangers), but it could misrepresent the physical processes occurring in open-loop schemes associated with substantial groundwater pumping.

Numerous studies performed in shallow sedimentary aquifers (<200 m) have shown the positive impact of advection in geothermal systems, which increases the thermal interaction between the host rock and pore water in cases of considerable groundwater flows (e.g., Russo and Taddia, 2010; Angelotti et al., 2014; Casasso and Sethi, 2014; Banks, 2015; Liuzzo-Scorpo et al., 2015; Smith and Elmore, 2018; Pophillat et al., 2020; Lou et al., 2021). Chiasson et al. (2000), demonstrated that advection increases the “effective thermal conductivity” of porous rocks for Peclet numbers around one or higher in layers of high hydraulic conductivity; a similar conclusion was reached by Liebel et al. (2012) and Abesser et al. (2021). Wang et al. (2009) showed an improved performance of heat exchangers (around 10%) with a strong groundwater flow, versus a no-flow scenario, with in-situ experiments in coarse sands and gravels. Ghoreishi-Madiseh et al. (2015), studying backfilled mine stopes in Canada, found that only in scenarios of a horizontal hydraulic conductivity higher than 10^–5 m/s, advection had a significant positive effect in the subsurface thermal exchange.

In this context, the graph of Figure 13 can be used for a preliminary assessment of the dominant heat transport mechanism in different hydrogeological settings. For the range of hydraulic gradients typically found in sedimentary basins (0.01–0.0001) heat conduction would be the dominant heat transport mechanism for most lithologies, including sandstones, and advection would have a central role in scenarios of very high hydraulic conductivity (>10^–5 m/s), representative of unconsolidated sands and gravels, as well as highly fractured rocks.

FIGURE 13. Relationship of hydraulic gradients and hydraulic conductivities present in typical geological scenarios with the possibility of advection as a significant mechanism for subsurface heat transport versus conduction (Ferguson, 2015).

Consequently, thermal storage schemes in flooded coal mines would benefit from the effect of local advection in the hydraulically enhanced rock volume, through an increase in heat transfer to and from the host rock. Thus, the scenarios analysed in this study, where conductive heat transport is exclusively modelled, could be considered a relatively moderate representation of the thermal performance of the host rock with respect to the influence of typical fracture and cleat networks around extraction panels. In the heat extraction phase, this would increase the heat retrieval from the host rock with cold-water refills, leading to higher temperatures in the extracted water.

Fracture networks around flooded panels could be simulated in future heat conduction models through an array of mesh elements of higher thermal conductivity surrounding the mine voids, with thickness related to the information of in-situ exploration surveys. Additionally, the possible hydraulic connection with other mine workings or with shallow aquifers, not modelled in this study, should be included (when appropriate) to account for possible thermal losses due to preferential pathways for advective heat transport.

Regarding the effect of the regional groundwater flow, mine-water schemes with multiple boreholes would benefit from advection through the transport of heat or cold away from the wells, preventing a local build-up of temperatures. Conversely, a strong regional groundwater flow could decrease the subsurface thermal efficiency through the dispersal of heat outside the planned heat extraction location, a process not included in the numerical models of this study. This detrimental process could be intensified by the increased “effective thermal conductivity” in the host rock, caused by the surrounding fracture networks, and lead to thermal plumes in the site. However, for mine-water thermal schemes in Carboniferous formations, the thermal plume development on a “site scale” outside the fractured-rock volume should be considerably smaller than the behaviour evidenced in shallow unconsolidated aquifers – where most thermal advection studies have been conducted (e.g., Fan et al., 2007; Meng et al., 2018)—given the much higher hydraulic conductivity of these sediments compared to highly compacted Carboniferous rocks. To prevent this negative outcome, strategies such as optimizing the well location according to the groundwater flow or placing the well screen so it induces thermal stratification, should be evaluated to increase the heat recovery (Jiang et al., 2019).

Model Properties and Boundary Conditions

The hydraulic conductivity and porosity of the host rock are primary parameters for the numerical simulation of geothermal systems in sedimentary environments. The relationship and combined role of these properties is often complex, given their potentially opposite effect for subsurface heat transport. According to Dehkordi and Schincariol (2014), higher porosities, associated with higher hydraulic conductivities, would reduce groundwater velocity and result in a diminished role of advective heat transport. On the other hand, higher porosities could enhance the thermal storage capacity of the system, as evidenced in the results of Figure 5, due to the exceptionally high specific heat capacity of water. Therefore, the impact of these decisive parameters (of typical high uncertainty) in the modelling results should be evaluated in sensitivity analyses (and calibrated with well data) for the determination of representative values for the specific host rock.

Another important aspect not assessed in this study, is the inclusion of a detailed layer configuration according to the stratigraphy typically found in Carboniferous sequences, which might contain intercalations of sandstones and organic shales. Given the contrasting thermal effect of these two rocks types, for instance, their inclusion in numerical models, when suitable, could have a large impact in the modelling results. Similarly, the contribution of the basal heat flow, the effect of different temperatures of the injected water and upward or downward groundwater flows could be modelled through Neumann boundary conditions in sensitivity analyses for the optimization of the scheme operation. Finally, other important conditions that could be incorporated in future real-world models include: potentially interconnected voids (e.g., shafts and roadways), different mining geometries (e.g., longwall extraction panels), material filling in subsurface voids and major faults located near the heat storage site.

Conclusion and Recommendations

The results of this numerical modelling study suggest that the efficiency of heat storage in flooded coal mines is highly sensitive to the geological conditions of the site, as the modelled minor lithological variation (2 m change in coal thickness) resulted in a 2-fold increase of the heat transferred to the subsurface in the 6-month heat storage phase. Conductive heat transport around the mine voids is largely controlled by the properties of rock-forming minerals and much less by the pore-water content of the host-rock. The presence of thermally conductive strata, such as clean sandstones, in the roof or base of mined coal seams (e.g., the Glasgow Main Coal) would be beneficial for the establishment of a thermal reservoir in the subsurface and could improve the seasonal heat recovery.

Up to 45% of the energy transferred to the host rock was retrieved in the first operational year with cold-water refills in the scenario of prospective subsurface conditions (Model A). The 5-year simulation shows that the energy recovery could easily exceed 50%, with moderate cold-water refill intervals, due to the progressive thermal increase in the subsurface produced by the heat injected seasonally. This transient evolution should be evaluated for the design of a suitable water circulation that prevents low, or even negative, energy yields in cases of low groundwater temperatures. The long-term forecast of the system suggests that it could be possible to attain the energy of the “mined” coal in less than 70 years with optimized heat extraction cycles. In financial terms, the cumulative heat recovered could equal a theoretical monetary value of the “mined” coal in less than 30 years, conditional to the energy price used.

Since operational mine-water thermal schemes are currently restricted to a small number of sites and no long-term experimental data exists for calibration, the results of this study provide a generic and broad perspective of the performance of this potential geothermal technology; particularly, regarding the maximum portion of energy potentially recoverable from the subsurface. For a more comprehensive assessment of thermal storage in legacy coal mines, future studies should include calibration with field data (when available), models with different mine geometries, the effect of the temperature increase of ground-source heat pumps, as well as the impact of local advection in the host rock and the thermal plume development caused by a considerable regional groundwater flow.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JP: methodology, validation, formal analysis, investigation, visualization, software, writing–original draft. CM: conceptualization, software, methodology, formal analysis, writing–review and editing. AFH: validation, writing–review and editing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References